图的构成

顶点集合+边的集合：G = (V, E)，顶点集合V = {x | x属于某个数据对象及}是有穷非空集合

E = {(x, y) | x, y属于V}或者E = {<x, y> | x, y属于V && Path(x, y)}是顶点间关系的有穷集合，也叫边集合
(x, y)表示x到y的一条双向通道，即(x, y)是无方向的，Path(x, y)表示从x到y的一条单向通路，即Path(x, y)是有方向的

顶点和边：图中节点成为顶点，第i个顶点记作vi，两个顶点vi和vj相关联称作顶点vi和顶点vj之间有一条边，图中第k条边记作ek，ek = (vi, vj)或ek = <vi, vj>

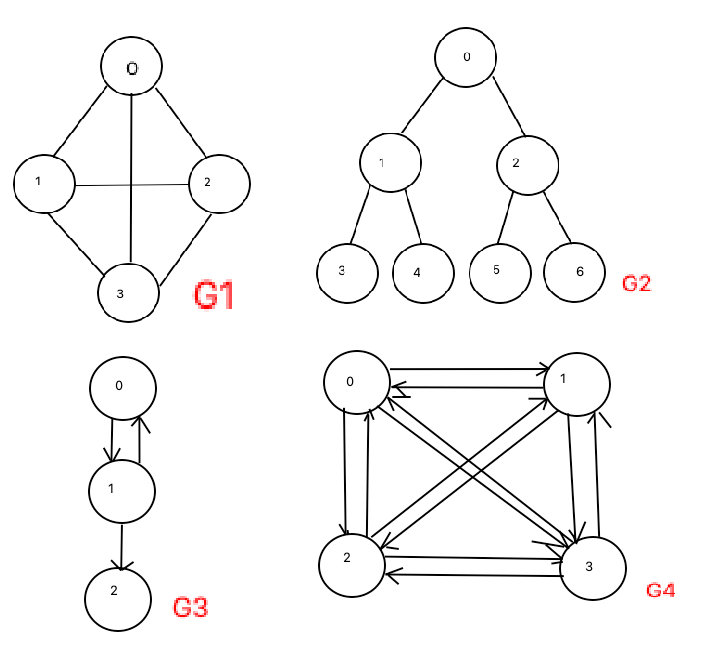
在有向图中，顶点对<x, y>是有序的，顶点对<x, y>称为顶点x到顶点y的一条边(弧)，<x, y>和<y ,x>是两条不同的边，如G3、G4
在无向图中，顶点对(x, y)是无序的，顶点对(x,y) 称为顶点x和顶点y相关联的一条边，这条边没有特定方向，(x, y)和(y，x)是同一条边，如G1、G2
注意：无向边(x, y)等于有向边<x, y>和<y, x>

可以表示：社交关系

社交关系中，每个人就是一个顶点，两个人是好友，他们之间就有了边，那么边的权值可以是他们的亲密度
无向图：QQ、微信类似的社交关系可以被看作是无向图（强社交关系，熟人社交）
有向图：微博（关注的关系）、抖音（弱社交关系，陌生人社交、粉丝社交）
也可以用来表示地图（导航路线选择），网络连接（路由器选择）
vertex 顶点、edge 边、weight 权值

图的存储结构

保存节点以及边的关系

邻接矩阵

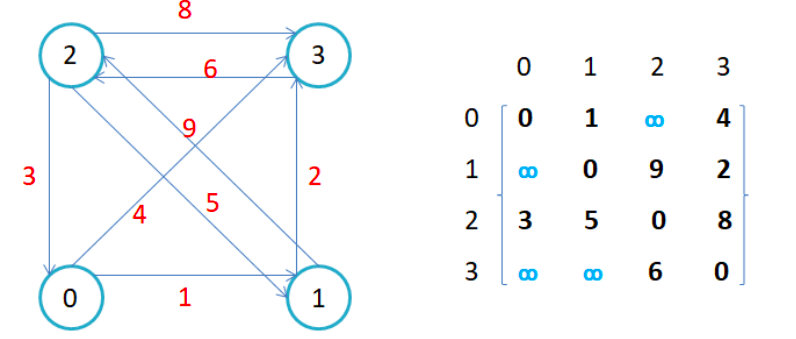
因为节点与节点之间的关系就是连通与否，即为0或者1，因此邻接矩阵(二维数组)即是：先用一个数组将顶点保存，然后采用矩阵来表示节点与节点之间的关系。

用vector<char> vertex保存顶点，用矩阵vector<vector<W> > edge保存边，如下

$edge = \left[ \begin{matrix} & A & B & C & D \\ A & 0 & 1 & 0 & 1 \\ B & 1 & 0 & 1 & 0 \\ C & 0 & 1 & 0 & 1 \\ D & 1 & 0 & 1 & 0 \end{matrix} \right]$

用vector<char> vertex保存顶点，用矩阵vector<vector<W> > edge保存边，如下

$edge = \left[ \begin{matrix} & A & B & C \\ A & 0 & 1 & 0 \\ B & 1 & 0 & 1 \\ C & 0 & 0 & 0\end{matrix} \right]$

无向图的邻接矩阵是对称的，第i行(列)元素之和，就是顶点i的度。有向图的邻接矩阵则不一定是对称的，第i行(列)元素之后就是顶点i 的出(入)度
如果边带有权值，并且两个节点之间是连通的，上图中的边的关系就用权值代替，如果两个顶点不通，则使用无穷大代替
用邻接矩阵存储图的有点是能够快速知道两个顶点是否连通，缺陷是如果顶点比较多，边比较少时，矩阵中存储了大量的0成为系数矩阵，比较浪费空间，并且要求两个节点之间的路径不是很好求。

邻接矩阵代码实现

//vertex 顶点
//edge 边
//weight 权值
//matrix矩阵

namespace matrix
{
    template<class V, class W, bool IsDirect = false>
    class Graph
    {
    public:
        Graph(V* vertexs, int n)
        {
            _vertexs.reserve(n);
            for(size_t i = 0; i < n; i++)
            {
                _vertexs.push_back(vertexs[i]);
                _vertexIndexMap[vertexs[i]] = i;
            }

            _matrex.resize(n);
            for(size_t i = 0; i < n; i++)
                _matrex[i].resize(n, W());
        }

        int GetVertexIndex(const V& v)
        {
            auto it = _vertexIndexMap.find(v);
            if(it != _vertexIndexMap.end())
                return it.second;
            else
                //return -1;
                throw invalid_argument("非法顶点");
        }

        //添加边
        void AddEdge(const V& src, const V& dst, const W& w)
        {
            int srcIndex = GetVertexIndex(src);
            int dstIndex = GetVertexIndex(dst);

            _matrex[srcIndex][dstIndex] = w;

            if(IsDirect == false)
                _matrex[dstIndex][srcIndex] = w;
        }

    private:
        vector<V> _vertexs;             //顶点集合
        map<V, int> _vertexIndexMap;    //表示顶点的下表映射关系
        vector<vector<W> > _matrex;     //表示邻接矩阵的边
    };
}

邻接表

使用数组表示顶点的集合，使用链表表示边的关系。

图为无向图的邻接表存储

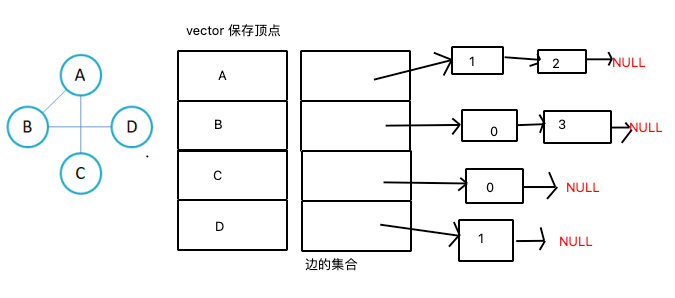
注意：无向图中同一条边在邻接表中出现了两次。如果想知道顶点vi的度，只需要知道顶点vi边链表集合中结点的数目即可
有向图则添加一个边的集合或者反向添加一次

邻接表的代码实现

namespace table
{
    template<class W>
    struct EdgeNode
    {
        int _srcIndex;
        int _dstIndex;
        const W& _w;

        EdgeNode<W>* _next;
    };

    template<class V, class W, bool IsDirect = false>
    class Graph
    {
    public:
        Graph(V* vertexs, int n)
        {
            _vertexs.reserve(n);
            for(size_t i = 0; i < n; i++)
            {
                _vertexs.push_back(vertexs[i]);
                _vertexIndexMap[vertexs[i]] = i;
            }

            _linkTable.resize(n, nullptr);
        }

        int GetVertexIndex(const V& v)
        {
            auto it = _vertexIndexMap.find(v);
            if(it != _vertexIndexMap.end())
                return it.second;
            else
                //return -1;
                throw invalid_argument("非法顶点");
        }

        //添加边
        void AddEdge(const V& src, const V& dst, const W& w)
        {
            int srcIndex = GetVertexIndex(src);
            int dstIndex = GetVertexIndex(dst);

            EdgeNode<W>* node = new EdgeNode<W>;
            node->_srcIndex = srcIndex;
            node->_dstIndex = dstIndex;
            node->_w = w;

            //挂起头
            node->_next = _linkTable[srcIndex];//链表的头插操作
            _linkTable[srcIndex] = node;

            if(IsDirect == false)
            {
                EdgeNode<W>* node = new EdgeNode<W>;
                node->_srcIndex = dstIndex;
                node->_dstIndex = srcIndex;
                node->_w = w;

                //挂起头
                node->_next = _linkTable[dstIndex];//链表的头插操作
                _linkTable[dstIndex] = node;
            }
        }

    private:
        vector<V> _vertexs;             //顶点集合
        map<V, int> _vertexIndexMap;    //表示顶点的下表映射关系
        vector<EdgeNode<W>*> _linkTable;//邻接表
    };
}

图的遍历

给定一个图G和其中任意一个顶点v0，从v0出发，沿着图中各边访问图中的所有顶点，且每个顶点仅被遍历一次。”遍历”即对结点进行某种操作的意思

图的深度优先遍历

对邻接矩阵，深度优先可是使用递归的方式实现

void _DFS(int srcIndex, vector<bool>& visited)
{
  cout << _vertexs[srcIndex] << ":" << srcIndex << "->";//输出当前节点
  visited[srcIndex] = true;//标记当前节点已访问
  for(size_t i = 0; i < _vertexs.size(); i++)
  {//访问当前节点的相邻顶点
    if(_matrex[srcIndex][i] != W() && visited[i] == false)
      _DFS(i, visited);
  }
}

void DFS(const V& src)
{
  vector<bool> visited(_vertexs.size(), false);
  int srcIndex = GetVertexIndex(src);
  _DFS(srcIndex, visited);
  cout << endl;
}

图的广度优先遍历

对邻接矩阵，广度优先可以使用队列实现

void BFS(const V& src)
{
  vector<bool> visited(_vertexs.size(), false);
  int srcIndex = GetVertexIndex(src);

  queue<int> q;
  q.push(srcIndex);

  while(!q.empty())
  {
    int front = q.front();
    q.pop();
    cout << _vertexs[front] << ":" << front << "->";
    //好友入队
    for(size_t i = 0; i < _vertexs.size(); i++)
    {
      if(visited[i] == false && _matrex[front][i] != W())
      {
        q.push(i);
        visited[i] = true;
      }
    }
  }

  cout << endl;
}

最小生成树

连通图中的每一棵生成树，都是原图的一个极大无环子图，即：从其中删去任何一条边，生成树就不再连通；反之，在其中引入任何一条新边，都会形成一条回路。

若连通图由n个顶点组成，则其生成树必含n个顶点和n-1条边。因此构造最小生成树的准则有三条：

只能使用图中的边来构造最小生成树
只能使用恰好n-1条边来连接图中的n个顶点
选用的n-1条边不能构成回路

构造最小生成树的方法：Kruskal算法和Prim算法。

这两个算法都采用了逐步求解的贪心策略。贪心算法：是指在问题求解时，总是做出当前看起来最好的选择。也就是说贪心算法做出的不是整体最优的选择，而是某种意义上的局部最优解。贪心算法不是对所有的问题都能得到整体最优解。

Kruskal算法

任给一个有n个顶点的连通网络N={V,E}
首先构造一个由这n个顶点组成、不含任何边的图G={V,NULL}，其中每个顶点自成一个连通分量
接着不断从E中取出权值最小的一条边(若有多条任取其一)，若该边的两个顶点来自不同的连通分量，则将此边加入到G中。
如此重复，直到所有顶点在同一个连通分量上为止。

核心：每次迭代时，选出一条具有最小权值，且两端点不在同一连通分量上的边，加入生成树。

如何判断选出一条边以后跟已有的边是否构成回路：并查集

如果选的边在一个集合中，就不能再使用，不在一个集合才能添加

Prime算法

仍是贪心算法，但它先选出最小的一条边，接着并非从全局中找到最小的边，而是以最小的边为基础，选已有的边的邻接顶点链接出的边中最小的，避开了选出环路的情况

单元最短路径

从在带权图的某一顶点出发，找出一条通往另一顶点的最短路径，最短也就是沿路径各边的权值总和达到最小。

Dijkstra算法和Floyd算法

Dijkstra算法

求一个点和图中的其他所有点之间的最路径

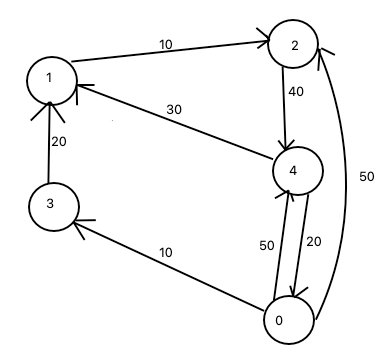
路径	路径长度
0，1	无穷大
0，2	50
0，3	10
0，4	50

依次遍历所有的边，找出更短路径，找到则更新

小赵的学习笔记

图