大模型构建-文本数据的处理

文本数据的处理，属于大模型的预训练阶段。通过使用下一单词预测任务，我们能够训练

那些拥有数百万甚至数十亿参数的大语言模型，从而打造出能力优异的模型。这些模型经过进一
步微调，便可以遵循通用指令或执行特定的目标任务。但是，在实现和训练大语言模型之前需要
先准备好训练数据集。

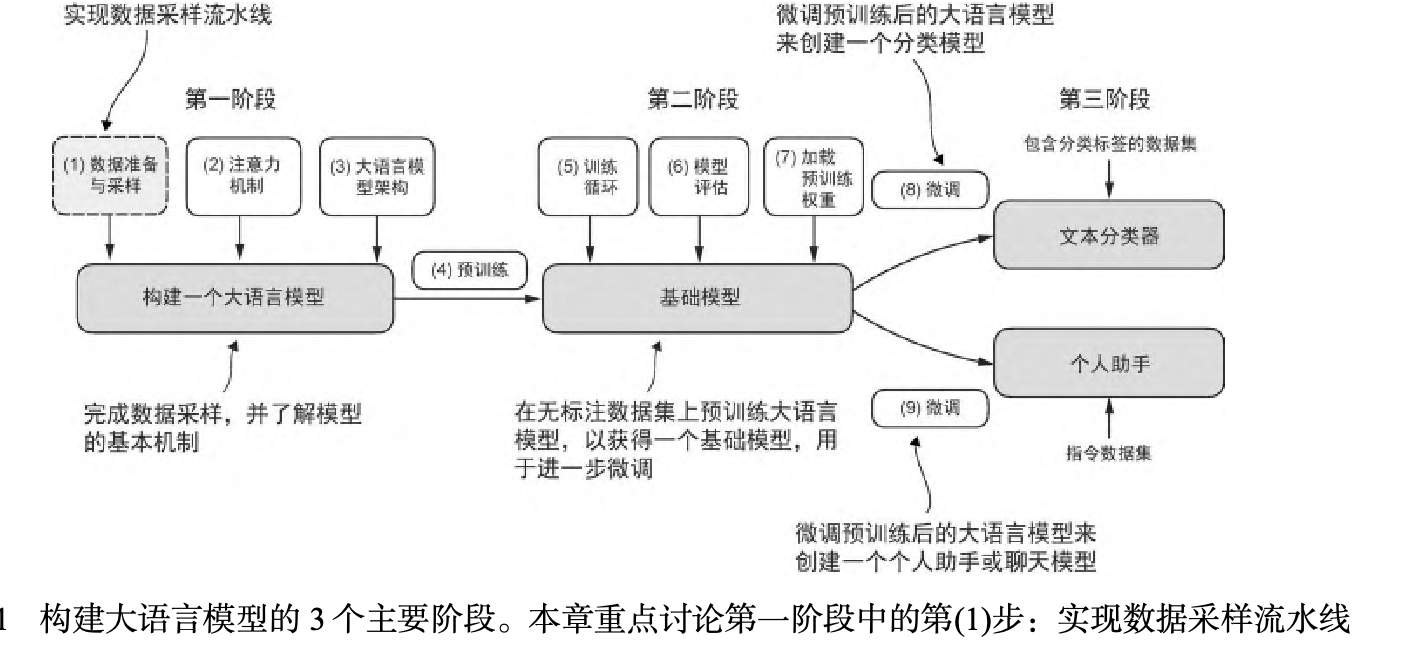
在后续的内容中，我们将学习如何为训练大语言模型准备输入文本。这涉及将文本分割为独立的单

​ 词词元和子词词元，然后将其编码为大语言模型所使用的向量表示。你还将了解到高级的分词技术，比如字节对编码（byte pair encoding，BPE） ，这是一种在 GPT 等流行的大语言模型中广泛使用的方法。最后，我们将实现一种采样和数据加载策略，来生成训练大语言模型所需的输入-输出对。

理解词嵌入（Embedding）

​ 在前面的章节中，我们得以了解大模型中有包含了的重要组成部分，编码器和解码器，那么到底什么是编码和解码，这里的码是什么？

​ 设想一个你从未听说过也从未见过的语言，而现在你需要学习它，我们应该如何开始？我们往往可以通过指定一个实体来映射不同语言之间的含义，例如

                        Banana =\=> 🍌 <=\= 香蕉

​ 但是机器无法理解实体的含义，我们没有办法让电脑知道什么是苹果，但我们仅依靠映射关系是不可行的，因为语言的组合可能性是无穷的。所以我们需要一个更加抽象的东西来描述这种映射关系，可以叫做语义，或者上下文。例如无论在哪种语言的大量文本中，香蕉一定伴随着 黄色/黑色/绿色、水果、甜/酸、食物 等词语出现，其在不同语境的上下文一定是相同的。而编码解码的码，就可以简单理解为将各种语言中的语法，发音，文字等形式上的不同剥离之后的纯语义关系

假如我们现在需要从头设计一个码，即表示语言中的语义，并且要能让计算机识别，那么可以简单的得到两个前提条件：

1. 语义的关系应该是数字化的，因为需要计算器来处理
2. 语义关系数字化之后的数值需要能体现出语义之间的关系，例如将所有的中文映射到一个三维空间中，香蕉和水果的距离一定是相近的，香蕉和月亮的距离一定是较远的（简陋的比喻一下）

在编码/解码之前，我们首先需要找到语言对应的基础的语义单元，可以是单词，字母，字，成语等等，而这个最基础的语义单元，在大模型领域被称为：Token

---

此处引入机器学习中的两个概念，分别是对语言中基础的语义单元进行数字化的两种方法：

• 标记器/分词器（tokenizer）：为每个Token分配一个独立的ID，相当于一个Token列表
• 独热编码（one hot）：为每个Token分配一个独立的维度，有多少Token就有多少维度

例如：

	tokenizer	one hot
苹果	1	1,0,0
香蕉	2	0,1,0
葡萄	3	0,0,1

但是以上两种数字化的方法，都难以完成大模型中编码的需求

• 对于tokenizer来说，所有的token都挤在一个数组中，信息过于密集，同时难以应对一次多义的情况，例如在tokenizer中，苹果，香蕉，葡萄等相近含义的词放在一起，看起来很合理，但如果此处的苹果是想指代苹果科技呢，此时就难以表达出苹果和手机，电脑等联系，亦或者我们想要表达苹果香蕉的复合语义时，如果直接将他们的ID相加得到的3此时已经被葡萄占用了。
• 对于独热编码来说，每个token独占一个维度，信息又过于稀疏了，虽然可以很好的表示组合语义（例如介于苹果和香蕉的词应该是1，1，0），但是难以体现Token之间的关系，由于每个token都独占一个维度，所有的token都相互正交，这就会导致苹果与香蕉间的距离，和苹果和步行之间的空间距离完全一致，独热编码的问题在于他的维度太高了。

‍

​ 以上两种方法可以看作是对文本数字化的两种极端场景，分词器的维度太低了，难以表示语义的组合，独热编码的维度太高了，难以表示不同语义的关系，那么应该怎么办呢？

能否找到一个，维度比分词器高，但是又没有独热编码高的空间来对文本进行编码，那对于以上两种编码方式我们可以选择：

1. 针对分词器编码结果升维
2. 针对独热编码结果降维

---

​ 直觉上来看，将高维的独热编码降低维度，似乎是一个较好的方案，毕竟概括比扩写更容易一点，如果要涉及到维度变换的操作，我们应该把目光投向更底层的数学原理，向量和矩阵的乘法

行向量和矩阵相乘：如果你有一个行向量 和一个矩阵 大小为 （ 是矩阵的行数， 是列数），则乘积 的结果是一个新的行向量，其大小为 。

$$\mathbf{v}A = [v_1, v_2, \dots, v_n] \cdot \begin{bmatrix} a_{11} & a_{12} & \dots & a_{1m} \\ a_{21} & a_{22} & \dots & a_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \dots & a_{nm} \end{bmatrix} = [\text{result}_1, \text{result}_2, \dots, \text{result}_m]$$

这里的每个 是行向量 和矩阵 的第 列的点积，例如

。

在上面的运算规则中，矩阵的行数代表转换前向量的维度，矩阵的列数代表转换后向量的维度，例如以下图式中包含两个维度：和

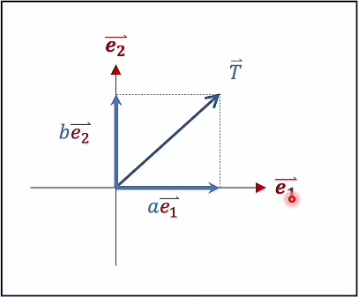
此时向量 ，而在新的坐标系中包含三个维度，此时向量应该如何在新的坐标系中表示？

我们需要先关注坐标轴之间的关系，因为向量在此处的值是什么并不重要，更需要关注坐标轴是如何变换

假设

• 原坐标 在新表坐标系的分量为
• 原坐标 在新表坐标系的分量为

则有

$$\vec{T} = a\vec{e_1}+b\vec{e_2}=a(w_{1,1},w_{1,2},w_{1,3})+b(w_{2,1},w_{2,2},w_{2,3})$$

而在新的坐标系中

$$\vec{T} = x\vec{e^{\prime}_1} + y\vec{e^{\prime}_2} + z\vec{e^{\prime}_3}$$

则有

$$\vec{T} \Rightarrow \begin{cases} x = aw_{1,1} + bw_{2,1} \\ y = aw_{1,2} + bw_{2,2} \\ z = aw_{1,3} + bw_{2,3} \end{cases}$$

按照向量的写法即为

$$\begin{bmatrix} a \\ b \end{bmatrix}^T \cdot \begin{bmatrix} w_{1,1} & w_{1,2} & w_{1,3} \\ w_{2,1} & w_{2,2} & w_{2,3} \end{bmatrix}$$

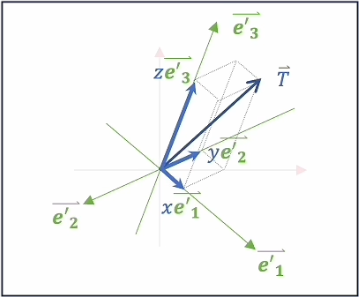
矩阵的行数代表转换前向量的维度，矩阵的列数代表转换后向量的维度，同时由于矩阵乘法的特点，原向量中的每个点和转换后向量中的每个点是一一对应的关系，因为只会发生旋转与拉伸，如果想要改变位置则需要借助向量的加法。

​ 也就是说，一个空间，经过矩阵运算后，会变成一个新的空间，而矩阵则是描述两个空间之间的变换规则，而如果是一组向量，也可以看作是矩阵和矩阵相乘，乘数矩阵可以看作是一个线性的变换规则，可以按照func 变换规则(原空间)新空间这样的黑盒去理解，写成数学表达式可以是，我们可以轻易的得出，在这之中重要的是矩阵，代表了空间变换的规则，神经网络中的隐藏层也就是对数据进行升维或降维的过程。

---

​ 有了以上的数学基础，我们现在来重新理解一下什么是Embedding，就是将文本里的Token变成独热码，然后再对其进行降维，也就是将输入内容根据语义投射到一个空间中，而这个过程由于是矩阵的乘法运算，所以将Token投入高维空间中的矩阵也被称为嵌入矩阵。在被投射到高维空间后，就剩下纯粹的数学运算了，不单单可以用于文本的翻译，也就是说，语言大模型在数学的层面上，他真的理解用户输入的是什么内容，而投射空间中的每一个维度都代表一个独立的基础的语义，例如某个维度代表色彩，某个维度代表气味等等。但是在实际操作中，AI模型自己学习到的特征可能是人类完全无法理解的。同时正因为空间具有连续的性质，不是简单的k-v对应关系，所以大模型可以去处理自己从未见到过的场景。

​ 那么新的问题出现了，我们如何获取到用来投射的嵌入矩阵，这里可以参照谷歌的word2vec，也是我们之前分享中提到的训练方法，它实现了根据目标词预测上下文，或根据上下文预测目标词，从而生成词嵌入。word2vec 的核心思想是，出现在相似上下文中的词往往具有相似的含义。因此，当这些词嵌入被投影到二维空间并进行可视化时，我们可以看到意义相似的词聚集在一起

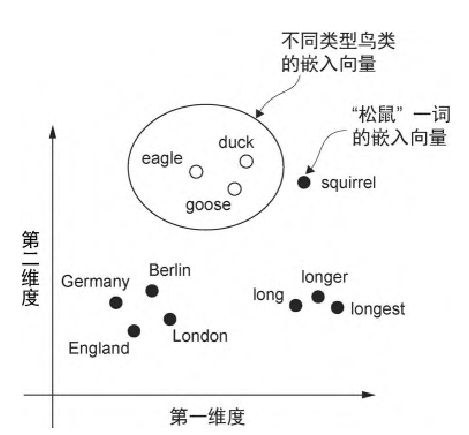
word2vec的目标不是得到某种结果，而是得到一种参数，用来将token映射到高维空间的方法，而在训练过程中，有以下两种方式：

• COBW：将一组奇数个向量中的某个向量挖空，让模型推测，也就是完形填空。例如：这是一个___苹果，这句话让模型预测，模型可以给出 甜，红，好吃的 这样的答案，这些预测都是正确的。但是即使模型给出了不同的正确的答案也没关系，因为我们的目的不是让模型去填空，而是获取到可以体现这些形容词和苹果的空间距离更近的语义关系。
• Skip-gram：给出一个向量，让模型拆解，反向的COBW

以上两种过程类似受力分析中的合力和分力，而word2vec所表达的更多的是一种客观性的语义关系，并且是根据输入的语料来决定的，它更像是编撰一本字典，但如果我们想要获取输入内容的主观语义，就需要注意力机制登场了。

不同Embedding之间的差异

大模型内的 embedding：

这是 ​模型的一部分（trainable parameter） 。

• 位置：Transformer 模型的输入第一层。
• 作用：把词元 ID 转为可训练的稠密向量（如 4096 维）。

• 性质：

  • 随模型一起训练。
  • embedding 向量最终学到的是 token 的“语义空间位置”。
  • 输出会被送进 Transformer 层（Attention、MLP 等）。

embedding 模型API

是一个​独立的、预训练好的模型，
专门用来把整段文本（或句子、段落）编码成一个语义向量。

• 输入：任意自然语言（”What is gold recycling?”）
• 输出：一个固定维度的语义向量（如 1536 维）
• 作用：语义检索、相似度搜索、聚类、RAG

它不是“模型中的一层”，而是一个独立的“服务模型”，
它自己内部当然也有一层 embedding，但输出的是整段文本的最终语义向量，这个向量可以拿去算相似度、存向量数据库，它 不会反向传播更新

文本的分词

​ 在上面理解词嵌入的过程中，我们可以知道，第一步是需要对文本进行分词以获取基础的语义单元：Token并为他们每一个都进行编号，这一步也被称作词元化处理，通常我们可以使用现成的分词器对文本进行处理

分词的效果演示：tiktokenizer.vercel.app

​ 在分词的过程中我们可以引入一些特殊的词元来辅助大模型对文本进行标记，例如<|unk|>词元来表示那些未出现在训练数据中，因而没有被包含在现有词汇表中的新词和未知词，<|endoftext|>词元来分隔两个不相关的文本来源。

​ 但是在GPT 模型使用的分词器并不依赖这些特殊词元，而是仅使用<|endoftext|>词元来简化其处理流程。<|endoftext|>词元与[EOS]词元作用相似。此外，<|endoftext|>也被用于文本的填充。然而，当模型在批量输入上进行训练时，我们通常使用掩码技术，这意味着我们并不会关注那些仅用于填充的词元。因此，具体选择哪种词元来进行填充实际上并不重要。此外，GPT 模型的分词器也不使用<|unk|>词元来处理超出词汇表范围的单词，而是使用BPE 分词器将单词拆解为子词单元如果分词器在分词过程中遇到不熟悉的单词，它可以将其表示为子词词元或字符序列

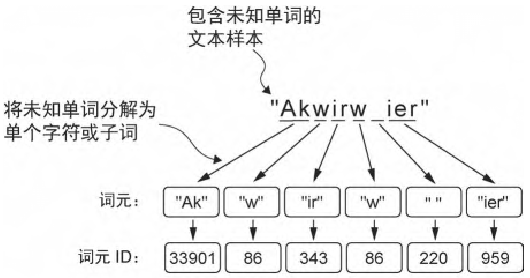
中文的分词效果

使用滑动窗口进行数据采样

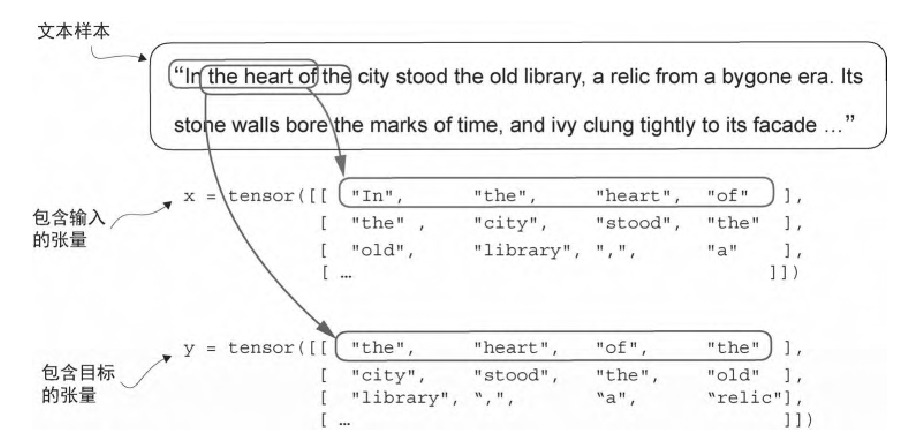
为了生成前文所述的嵌入矩阵，我们需要为大模型准备用于训练的输入-目标对，例如

这里其实就是在借鉴word2vec的方法，为模型生成用于完形填空的“试题”，我们可以使用滑动窗口的方法来达成这一目标，利用python包pyTorch中的Dataset与Dataloader来快速实现这一目的，例如

class GPTDatasetV1(Dataset):
    def __init__(self, txt, tokenizer, max_len, stride):
        self.input_ids = []
        self.target_ids = []

        token_ids = tokenizer.encode(txt)

		# 使用滑动窗口将文本划分为长度为max_len的重叠序列
		# 以下range表示为从0开始，len(token_ids) - max_len结束，步长stride
        for i in range(0, len(token_ids) - max_len, stride):
            input_chunk = token_ids[i:i+max_len]
            target_chunk = token_ids[i+1:i+max_len+1]
            self.input_ids.append(torch.tensor(input_chunk))
            self.target_ids.append(torch.tensor(target_chunk))

    def __len__(self): # 返回数据集总行数
        return len(self.input_ids)

    def __getitem__(self, index): # 返回数据集的指定航
        return self.input_ids[index], self.target_ids[index]

def create_dataloader_v1(txt, batch_size=4, max_len=256, stride=128, shuffle=True, drop_last=True, num_workers=1):
    tokenizer = tiktoken.get_encoding("gpt2")
    dataset = GPTDatasetV1(txt, tokenizer, max_len, stride)
    return DataLoader(
        dataset,
        batch_size=batch_size,
        shuffle=shuffle,
        drop_last=drop_last,
        num_workers=num_workers)

def main():
    with open("the-verdict.txt", "r", encoding="utf-8") as f:
        raw_txt = f.read()
    dataloader = create_dataloader_v1(
        raw_txt,batch_size=1, max_len=4,stride=1,shuffle=True)
    data_iter = iter(dataloader)

    first_batch = next(data_iter)
    print(first_batch)

最终达成下图的效果

创建词元嵌入

为大语言模型准备输入文本的最后一步是将词元ID转换为嵌入向量，这一步可以理解为是将词元ID作为独热编码的维度进行降维，例如

# 创建一个只包含4个ID的词元列表
input_ids = torch.tensor([2, 3, 5, 1])

vocab_size = 6 # 词元ID总数为6，可以理解为一个6维的独热编码
output_dim = 3 # 创建一个维度为3的嵌入矩阵

torch.manual_seed(123) # 设置随机种子
embedding_layer = torch.nn.Embedding(vocab_size, output_dim) # 嵌入操作
print(embedding_layer.weight)

以上的输出内容为

Parameter containing:
tensor([[ 0.3374, -0.1778, -0.1690], # 词元ID=0的嵌入向量
        [ 0.9178,  1.5810,  1.3010], # 词元ID=1的嵌入向量
        [ 1.2753, -0.2010, -0.1606], # 词元ID=2的嵌入向量
        [-0.4015,  0.9666, -1.1481], # 词元ID=3的嵌入向量
        [-1.1589,  0.3255, -0.6315], # ...
        [-2.8400, -0.7849, -1.4096]], requires_grad=True)

有一点需要特别强调一下，当前生成的嵌入向量其实是按照正态分布随机生成的，专门用于通过词元ID查找嵌入向量的

例如输入 6，3 就会生成 ；6 行 3 列 的随机矩阵，输入3，6就会生成 3 行 6 列，这一过程是相当于给一个初始的随机值

而在随后的训练中，会逐渐调整内容，让其复合词元ID的含义

也就是先建一个 vocab_size × embedding_dim 的随机矩阵，等着训练来优化它

模型的输入是将文本转换为词元ID，接着将词元ID作为独热编码的高位向量，通过嵌入矩阵将其降维，而torch.nn.Embedding则是一步到位，直接生成一个随机的已经降维的向量集合矩阵

我们现在有词元ID列表 ，想要获取词元ID为3的嵌入向量

先将其转换为独热编码 ，接着将其和嵌入矩阵相乘

$$\mathbf{v}A = \begin{bmatrix} 0 & 0 & 1 & 0 & 0 & 0 \end{bmatrix} \cdot \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ a_{41} & a_{42} & a_{43} \\ a_{51} & a_{52} & a_{53} \\ a_{61} & a_{62} & a_{63} \end{bmatrix} = \begin{bmatrix} a_{31} & a_{32} & a_{33} \end{bmatrix}$$

词元的嵌入操作并不是像其他层（如线性层、卷积层）那样依赖矩阵乘法进行变换，而是通过查找操作直接从预先初始化的嵌入矩阵中提取词元的嵌入向量。这个过程本质上是一个查询操作，不是传统意义上的“计算”，例如在以上基础下执行

vocab_size = 6  # 词元ID总数为6
   output_dim = 3  # 创建一个维度为3的嵌入矩阵

   torch.manual_seed(123)  # 设置随机种子
   embedding_layer = torch.nn.Embedding(vocab_size, output_dim)
   print(embedding_layer.weight)
   print(embedding_layer(torch.tensor([3])))

将会输出

tensor([[ 0.3374, -0.1778, -0.1690],
        [ 0.9178,  1.5810,  1.3010],
        [ 1.2753, -0.2010, -0.1606],
        [-0.4015,  0.9666, -1.1481], # 词元ID=3的嵌入向量
        [-1.1589,  0.3255, -0.6315],
        [-2.8400, -0.7849, -1.4096]], requires_grad=True)
tensor([[-0.4015,  0.9666, -1.1481]], grad_fn=<EmbeddingBackward0>)

或者输入

print(embedding_layer(torch.tensor([2,3])))

Parameter containing:
tensor([[ 0.3374, -0.1778, -0.1690],
        [ 0.9178,  1.5810,  1.3010],
        [ 1.2753, -0.2010, -0.1606], # 词元ID为2的嵌入向量
        [-0.4015,  0.9666, -1.1481], # 词元ID为3的嵌入向量
        [-1.1589,  0.3255, -0.6315],
        [-2.8400, -0.7849, -1.4096]], requires_grad=True)
tensor([[ 1.2753, -0.2010, -0.1606],
        [-0.4015,  0.9666, -1.1481]], grad_fn=<EmbeddingBackward0>)

在训练过程中，嵌入矩阵中的权重会更新。这种更新发生在反向传播阶段。每个词元的嵌入向量会根据损失函数和梯度下降算法进行更新，使得它们能够更好地表示词元的语义信息。

编码单词位置信息

嵌入层的工作机制是，无论词元 ID 在输入序列中的位置如何，相同的词元 ID 始终被映射到相同的向量表示，例如

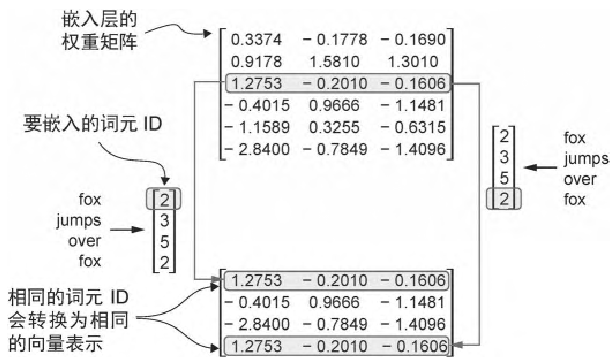
原则上，带有确定性且与位置无关的词元 ID 嵌入能够提升其可再现性。然而，由于大语言

模型的自注意力机制本质上与位置无关，因此向模型中注入额外的位置信息是有帮助的。

为了实现这一点，可以采用两种位置信息嵌入策略：绝对位置嵌入和相对位置嵌入。

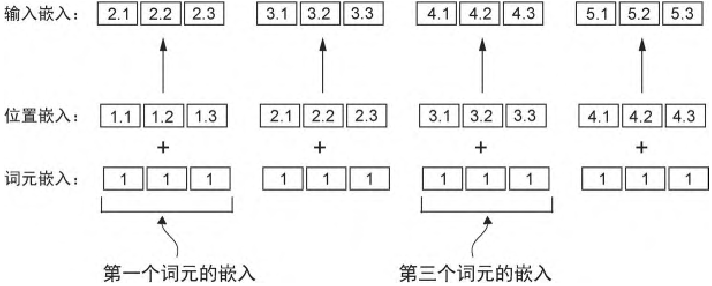
• 绝对位置嵌入（absolute positional embedding）直接与序列中的特定位置相关联。对于输入序列的每个位置，该方法都会向对应词元的嵌入向量中添加一个独特的位置嵌入，以明确指示其在序列中的确切位置。例如，序列中的第一个词元会有一个特定的位置嵌入，第二个词元则会有另一个不同的位置嵌入，以此类推，如下图

  

  通常，绝对位置嵌入在Transformer模型中是通过位置嵌入矩阵来实现的。这个矩阵的大小为 [max_len, embedding_dim]​，其中 max_len​ 是最大序列长度，embedding_dim​ 是嵌入向量的维度。每个位置的嵌入是通过位置索引来索引嵌入矩阵获得的

• 相对位置嵌入（relative positional embedding）关注的是词元之间的相对位置或距离，而非它们的绝对位置。这意味着模型学习的是词元之间的“距离”关系，而不是它们在序列中的“具体位置” 。这种方法使得模型能够更好地适应不同长度（包括在训练过程中从未见过的长度）的序列。

‍

以上两种位置嵌入都旨在提升大语言模型对词元顺序及其相互关系的理解能力，从而实现

更准确、更具上下文感知力的预测。选择使用哪种嵌入策略，通常取决于具体的应用场景和数据
特性。OpenAI 的 GPT 模型使用的是绝对位置嵌入，这些嵌入会在训练过程中被优化，有别于原始Transformer 模型中的固定或预定义位置编码。

接下来上点真家伙

前面我们使用了非常小的嵌入维度。现在，我们将考虑更实际、更实用的嵌入维度，将输入的词元编码为 256 维的向量表示。虽然这个维度仍比原始 GPT-3 模型的维度（GPT-3 模型的嵌入维度为 12 288）要小，但对实验来说是合理的。

import tiktoken
import torch
from torch.utils.data import Dataset,DataLoader

class GPTDatasetV1(Dataset):
    def __init__(self, txt, tokenizer, max_len, stride):
        self.input_ids = []
        self.target_ids = []

        token_ids = tokenizer.encode(txt)

        for i in range(0, len(token_ids) - max_len, stride):
            input_chunk = token_ids[i:i+max_len]
            target_chunk = token_ids[i+1:i+max_len+1]
            self.input_ids.append(torch.tensor(input_chunk))
            self.target_ids.append(torch.tensor(target_chunk))

    def __len__(self):
        return len(self.input_ids)

    def __getitem__(self, index):
        return self.input_ids[index], self.target_ids[index]

def create_dataloader_v1(txt, batch_size=4, max_len=256, stride=128, shuffle=True, drop_last=True, num_workers=1):
    tokenizer = tiktoken.get_encoding("gpt2")
    dataset = GPTDatasetV1(txt, tokenizer, max_len, stride)
    return DataLoader(
        dataset,
        batch_size=batch_size,
        shuffle=shuffle,
        drop_last=drop_last,
        num_workers=num_workers)

def main():
    with open("the-verdict.txt", "r", encoding="utf-8") as f:
        raw_txt = f.read()
    max_len = 4
    dataloader = create_dataloader_v1(
        raw_txt,
		batch_size=8, # 每个批次加载 8 个样本
		max_len=max_len, # 每个样本的最大长度为 4
		stride=max_len, # 滑动窗口的步长为 4，意味着每次生成一个新样本时，都会从上一个样本的结尾位置开始，保持步长为 4
		shuffle=False) # 数据不会进行随机打乱
    data_iter = iter(dataloader)
    inputs, targets = next(data_iter)

    # print("Token IDs:\n", inputs)
    # print("\nInputs shape:\n", inputs.shape)

    vocab_size = 50257
    output_dim = 256
    # 生成256维的嵌入向量矩阵
    token_embedding_layer = torch.nn.Embedding(vocab_size, output_dim)
    token_embeddings = token_embedding_layer(inputs)
    # print(token_embeddings.shape)

	# 绝对位置嵌入
    context_length = max_len
	# 创建一个位置嵌入层，这个嵌入层的大小是 [max_len, output_dim]，
	# 也就是 [max_len, 256]。每个位置（从 0 到 max_len-1）会被
	# 映射到一个 256 维的嵌入向量
    pos_embedding_layer = torch.nn.Embedding(context_length, output_dim)
    pos_embeddings = pos_embedding_layer(torch.arange(context_length))
    # print(pos_embeddings.shape)

    input_embeddings = token_embeddings + pos_embeddings

最终的 input_embeddings​ 是每个词元的 词嵌入 与该词元在文本中的 位置嵌入 相加的结果。这是模型的输入，包含了两个方面的信息：

• 词元的 ​语义信息（通过词嵌入表示）。
• 词元在序列中的 ​位置关系（通过位置嵌入表示）。

在以上代码中：

• ​token_embeddings​：将每个词元ID映射到一个 256 维的词嵌入向量，表示词元的语义信息。
• ​pos_embeddings​：为每个位置生成一个 256 维的位置嵌入向量，表示该位置在序列中的相对位置。
• ​input_embeddings​​：将 token_embeddings​ 和 pos_embeddings 相加，生成最终的输入嵌入。这个嵌入包含了词元的语义信息和其位置的顺序信息，作为模型的输入。

‍